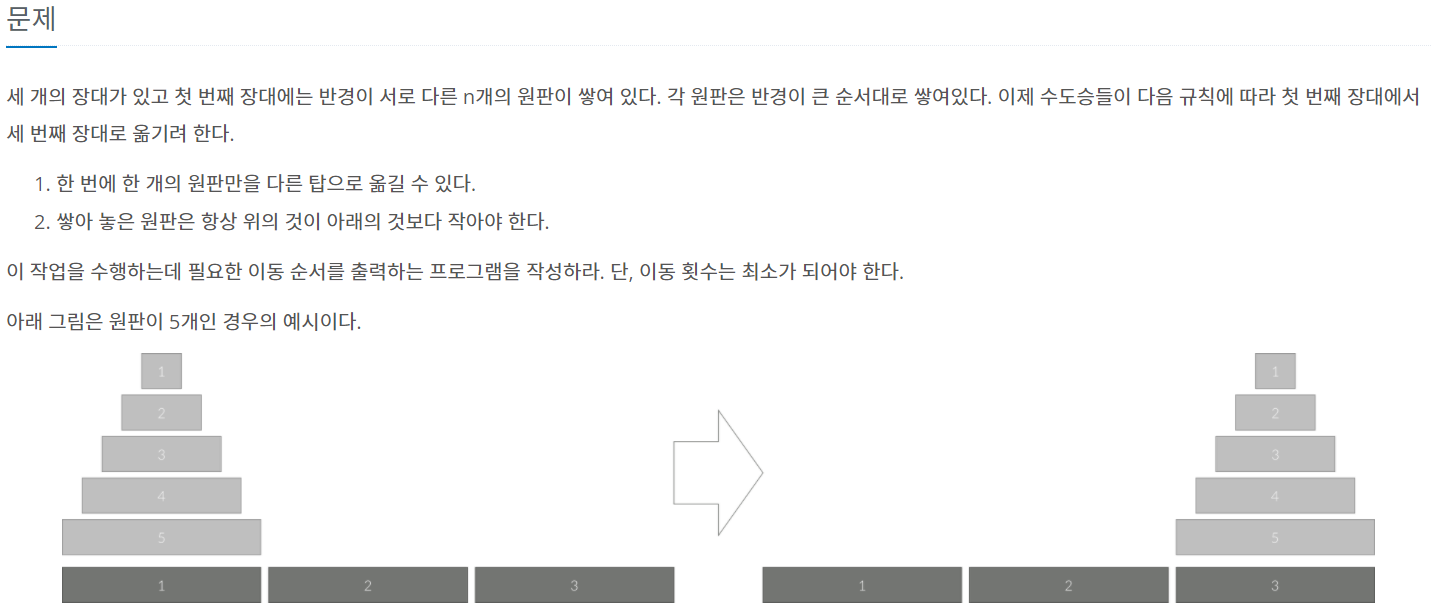

<풀이>
하노이 탑의 해결 방법을 생각해보면 재귀적이다.

위의 gif처럼 1~6번 원판을 첫 번째 장대에서 세 번째 장대로 옮기기 위해서는 먼저 1~5번 원판을 두번째로 옮긴 후 6번 원판을 세 번째 장대로 옮겨야한다. 이렇게 되면 문제는 1~5번 원판을 두 번째 장대에서 세 번째 장대로 옮기는 문제로 바뀐다.
즉, 재귀는 자기보다 작은 규모의 문제를 먼저 해결하고 그것을 자기의 문제에 이용하는 것이다.
재귀는 Base Case + Recursive Case로 이루어져있다.
Base Case는 if문 안의 부분이며 바닥에 닿았을 때 재귀를 끝내는 경우이다.
Recursive Case는 else 안의 부분이며 재귀적으로 반복하게 하는 경우이다.
위 용어를 바탕으로 정리하면,
1. Recursive Case의 경우 Recursive하게 호출하는 내 자신 메소드가 해결하고자 하는 문제가 항상 내가 해결하고자 하는 문제보다 작은지를 확인해야한다.
2. 그리고 이 작은 문제가 Recursive하게 갔을 때 최종적으로 Base Case에 도달할 수 있어야 한다.
def hanoi(num, from_, to, other):
if num == 0: return # base case
hanoi(num-1, from_, other, to)
print(from_, to)
hanoi(num-1, other, to, from_)하노이 탑 함수는 위와 같이 구성된다.
(num : 원판의 개수 / from_ : 시작하는 장대 번호 / to : 옮기려는 장대 번호 / other : 나머지 하나 남은 장대 번호)
if 문의 값은 base case로 원판이 0개 남으면 그대로 return해서 부모 노드로 올라간다.
그리고 밑의 코드를 위에서 본 gif 상황을 가정해두고 설명하면 num이 6이라고 할 때, 6번 원판이 없다고 생각하고(잠깐 빼놓았다고 생각하자) 1~5번 원판을 첫 번째 장대에서 두 번째 장대로 옮긴다고 생각하는 거다.
그걸 코드로 옮기면 hanoi(num-1, from_, other, to)이다.
그리고 방금 없다고 생각했던 6번 원판을 세 번째 장대로 옮긴다. 이것이 print(from_, to)이다.
마지막으로 두 번째 장대에 옮겨두었던 1~5번 원판을 6번 원판 위, 즉 세 번째 장대위로 다시 옮긴다. 그러면 우리가 원하는 대로 첫 번째 장대에서 세 번째 장대로 옮길 수 있을 것이다. 이걸 코드로 옮기면 hanoi(num-1, other, to, from_)이다.
재귀를 그려보면 결국 트리형태로 나오게 되는데 위와 같이 함수를 작성하면 트리를 InOrder로 순회하게 된다.
InOrder 순회는 아래와 같다.
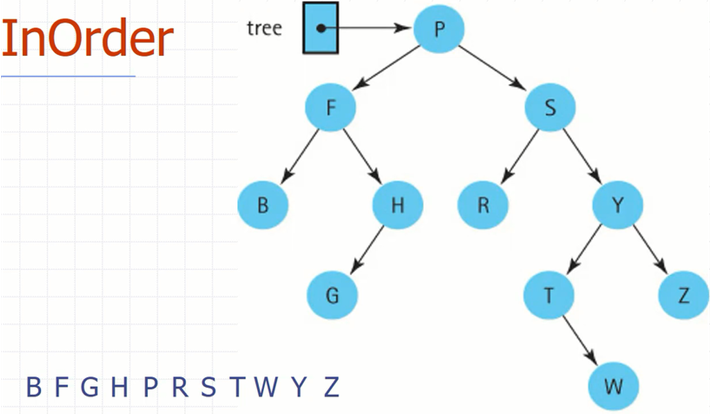
InOrder말고도 대표적으로 PreOrder, PostOrder과 같은 순회방법이 있다.

PreOrder은 부모 노드먼저 순회하고, PostOrder은 자식들 먼저 순회하고, InOrder은 왼쪽에서 오른쪽으로 순회한다고 생각하면 된다.
다시 문제로 돌아오면 위 코드는 InOrder 순회를 하게함으로써 해결할 수 있었다.
전체 코드를 적어보면 아래와 같다.
N = int(input())
def hanoi(num, from_, to, other):
if num == 0: return # base case
hanoi(num-1, from_, other, to)
print(from_, to)
hanoi(num-1, other, to, from_)
print(2**N - 1) # 하노이탑 최소 이동 횟수 출력
hanoi(N, 1, 3, 2)
<핵심 정리>
1. 재귀는 트리의 형태로 표현한다. 어떤 방식으로 순회할 지를 생각해서 코드 짜면 된다.
2. 재귀는 자기보다 작은 규모의 문제를 먼저 해결하고 그것을 자기의 문제에 이용하는 것이다.
3. Base Case + Recursive Case
'Base > Algorithm Study' 카테고리의 다른 글
| [Python/파이썬] 백준 알고리즘 15649번 - N과 M (1) (BackTracking) (0) | 2022.03.01 |
|---|---|
| [Python/파이썬] 백준 알고리즘 7576번 - 토마토 (BFS) (0) | 2022.03.01 |
| [Python/파이썬] 백준 알고리즘 1260번 - DFS와 BFS (0) | 2022.02.25 |
| [Python/파이썬] 백준 알고리즘 11052번 - 카드 구매하기 (DP) (0) | 2021.08.25 |
| [Python/파이썬] 백준 알고리즘 11726번 - 2×n 타일링 (DP) (0) | 2021.08.24 |