
Insertion sort, Selection sort, Bubble sort은 모두 시간 복잡도가 O(n^2)으로 한 family의 알고리즘이라고 한다.
이들을 가지고 '백준 알고리즘 2750번 - 수 정렬하기' 문제를 풀어보겠다.

물론 파이썬의 내장함수를 쓸 수도 있다.
하지만 문제의 의도가 그것이 아니기 때문에 정렬 알고리즘들을 가지고 풀어보겠다.
<풀이 1 - Insertion Sort>
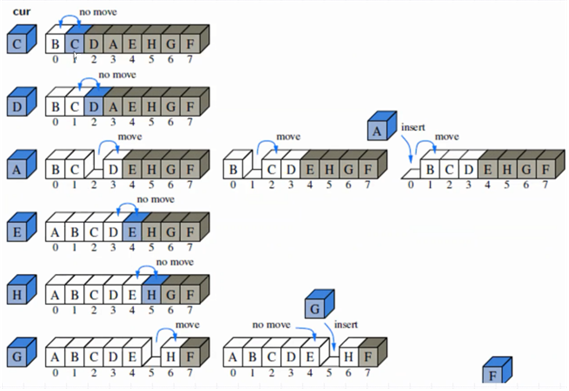
Insertion Sort 알고리즘은 위와 같은 개념으로 정렬되는 알고리즘이다.
### < Insertion Sort >
N = int(input())
result = []
for _ in range(N):
result.append(int(input()))
for i in range(1, N):
cursor = result[i]
j = i
while j > 0 and result[j-1] > cursor:
result[j] = result[j-1]
j -= 1
result[j] = cursor
for k in range(N):
print(result[k])for _ in range(N): 을 통해 result라는 리스트에 정렬해야 할 수들을 추가한다.
이제 for i in range(1, N): 부터가 Insertion Sort 알고리즘이다.
cursor변수에 값을 넣어놓고 cursor 바로 앞 인덱스부터 값을 서로 비교한다.
그리고 만약 그 수가 cursor의 값보다 크다면 순서를 바꾼다.
이를 반복해서 만약 cursor 값보다 작은 값이 앞에 나타났거나, 인덱스 0 자리에 도달했다면 그 자리에 cursor의 값을 넣는다.
마지막 for문인 for k in range(N): 은 result 리스트에 있는 값들을 차례로 출력하는 코드이다.
<풀이 2 - Selection Sort>

Selection Sort 알고리즘은 위와 같은 개념으로 정렬되는 알고리즘이다.
### < Selection Sort >
N = int(input())
result = []
for _ in range(N):
result.append(int(input()))
for i in range(N-1):
minNumIdx = i
for j in range(i+1, N):
if result[minNumIdx] > result[j]:
minNumIdx = j
temp = result[i]
result[i] = result[minNumIdx]
result[minNumIdx] = temp
for k in range(N):
print(result[k])아까와 똑같이 for _ in range(N): 을 통해 result라는 리스트에 정렬해야 할 수들을 추가한다.
이제 for i in range(N-1): 부터가 Selection Sort 알고리즘이다.
i는 sorted group에 포함될 인덱스를 의미한다.
먼저 가장 작은 숫자의 인덱스를 i로 가정해둔다.
그리고 i+1번째 인덱스부터 리스트의 끝까지 조사하며 가장 작은 수를 찾는다.
그래서 그 수와 인덱스 i번째 수를 교체하는 것이다.
마지막 for문인 for k in range(N): 은 result 리스트에 있는 값들을 차례로 출력하는 코드이다.
<풀이 3 - Bubble Sort>

Bubble Sort 알고리즘은 위와 같은 개념으로 정렬되는 알고리즘이다.
Bubble Sort를 생각할 때는 리스트를 세로로 세워놓고 많이 생각하는데, 거품이 보글보글 위로 올라가는 것처럼 정렬된다고 해서 그렇다.
### < Bubble Sort >
N = int(input())
result = []
for _ in range(N):
result.append(int(input()))
for i in range(N): # i는 이번에 sort 될 자리이다.
for j in range(N-1, i, -1):
if result[j] < result[j-1]:
temp = result[j]
result[j] = result[j-1]
result[j-1] = temp
for k in range(N):
print(result[k])이번에도 마찬가지로 for _ in range(N): 을 통해 result라는 리스트에 정렬해야 할 수들을 추가한다.
이제 for i in range(N): 부터가 Bubble Sort 알고리즘이다.
i는 sorted group에 포함될 인덱스를 의미한다.
그리고 이 Bubble Sort는 리스트의 뒤쪽 인덱스부터 시작해서 앞쪽으로 온다. (for j in range(N-1, i, -1): N-1부터 i+1번째까지 역순으로 for문을 돌리는 것이다.)
그리고 if문으로 j번째 인덱스와 그 앞쪽 인덱스인 j-1번째 인덱스의 값을 비교해 만약 앞쪽의 수가 더 크다면 교체한다.
마지막 for문인 for k in range(N): 은 result 리스트에 있는 값들을 차례로 출력하는 코드이다.
이렇게 시간 복잡도가 O(n^2)인 정렬 알고리즘들을 살펴보았다.
이 알고리즘들은 시간 복잡도가 너무커서 정렬해야 할 수가 커지면 계산 시간이 무지막지하게 커진다는 단점이 있다.
하지만 구현이 쉽다는 장점이 있어 종종 사용된다.
'Base > Algorithm Study' 카테고리의 다른 글
| [Python/파이썬] 백준 알고리즘 1181번 - 단어 정렬 (0) | 2021.08.20 |
|---|---|
| [Python/파이썬] 백준 알고리즘 11651번 - 좌표 정렬하기 2 (0) | 2021.08.19 |
| [Python/파이썬] 백준 알고리즘 7568번 - 덩치 (2) | 2021.08.17 |
| [Python/파이썬] 백준 알고리즘 1929번 - 소수 구하기 (0) | 2021.08.17 |
| [Python/파이썬] 백준 알고리즘 2869번 - 달팽이는 올라가고 싶다 (0) | 2021.08.16 |